REBAJAR PESO
LA IMPORTANCIA DE UNAS RUEDAS LIGERAS
El peso de una bici (o el de algunas de sus piezas) es un tema recurrente en el mundillo ciclista, y a la vez fuente de agrias disputas. Todos la quieren lo más ligera posible, pero pocos hacen un balance real de lo que se gana y la merma en prestaciones que supone usar componentes que transmiten peor las fuerzas o que empeoran la maniobrabilidad de la bici. Es difícil cuantificar la relación peso bici-ciclista idónea, es mejor fiarse de la experiencia y quedarnos con una bici con la que nos sintamos cómodos antes que con una absurda bici de muestrario.
Así pues, esta entrada no hablará de si se nota realmente la rebaja de peso en el rendimiento del ciclista, sino más bien de dónde conviene rebajar peso en caso de que queramos hacerlo.
La frase más escuchada y errónea es la siguiente: “donde más se nota la rebaja de peso es en las partes móviles”. Esto es falso, a efectos prácticos, sólo se nota la disminución de peso en el perímetro exterior de la rueda. No en otras piezas de la bici o partes de la misma rueda aunque se estén “moviendo”.
Voy a justificarlo con un pequeño análisis usando el momento de inercia, que según la wikipedia es el valor escalar del momento angular de un sólido rígido. Nos ayudará a demostrarlo porque es una magnitud que refleja la distribución de masas de un cuerpo o un sistema de partículas, respecto de un eje, en un movimiento de rotación. Para un cuerpo de masa continua se formula como:
 (*)
(*)
Haremos un balance de energía cinética de la pieza en cuestión (rueda, pedales, bielas, disco…).
La energía cinética total de un sólido rígido en rotación puede descomponerse como suma de la energía cinética de traslación (que es la asociada al desplazamiento del centro de masa del cuerpo a través del espacio) y la energía cinética de rotación (que es la asociada al movimiento de rotación con cierta velocidad angular). La expresión matemática para la energía cinética es:
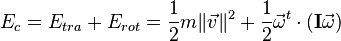
Donde:
 Energía de traslación
Energía de traslación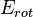 Energía de rotación
Energía de rotación masa del cuerpo
masa del cuerpo tensor de (momentos de) inercia
tensor de (momentos de) inercia velocidad angular del cuerpo
velocidad angular del cuerpo traspuesta del vector de la velocidad angular del cuerpo
traspuesta del vector de la velocidad angular del cuerpo velocidad lineal del cuerpo
velocidad lineal del cuerpoComo primer ejercicio vamos a calcular la energía cinética de una rueda (dibujo1) simplificando la distribución de su masa (dibujo2), concentrándola en un radio R=0.3 m y m=1.2 kg, suma del peso de la llanta (400 g)+cubierta(650 g)+otros(150 g de las cabecillas, sellante, etc). Los radios y buje los supondremos despreciables, hipótesis que debe ser verificada, sino habría que incluirlas en el modelo y repetir su análisis.


Si el ciclista va a 25 km/h (6.94 m/s) se tiene:
 = 1/2*m*v^2 = 0.5*1.2*(6.94)^2 = 28.9 J
= 1/2*m*v^2 = 0.5*1.2*(6.94)^2 = 28.9 J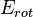 = 1/2*I*w^2 = aprox (*) =1/2*m*R^2*w^2= 1/2*m*v^2 = 28.9 J
= 1/2*I*w^2 = aprox (*) =1/2*m*R^2*w^2= 1/2*m*v^2 = 28.9 JEn este último cálculo habría que haber resuelto la integral (*) pero como hemos simplificado el modelo de rueda la integral queda fácil, I=m*R^2. Además se ha hecho uso de la definición w=v/R, por lo que al final vuelve a quedar la misma fórmula para ambas energías (realmente si hiciésemos la integral de los radios y el toro que es la rueda nos daría un valor algo más bajo en julios para
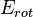 que el que nos sale para
que el que nos sale para  ).
).Así podemos concluir que la energía se reparte a partes iguales entre la de rotación y la de traslación. Es decir, que la rueda porta el doble de energía que otra pieza suspendida y misma masa (un cuadro que pese 1.2 kg, por ejemplo). Es por lo que algunos dicen que el peso de las ruedas cuenta doble. No es así exactamente, pero aceptemos pulpo como animal de compañía Digo esto porque aunque energéticamente es cierto, las ruedas son todavía más importantes si hacemos un estudio de aceleraciones (sólo hemos supuesto velocidad constante).
Como segundo ejercicio podemos analizar el fenómeno inercial en otras partes de la bici como pedales, bielas o rotores. ¿Tendrán la misma importancia?
En el estudio de bielas/pedales, observamos que el peor de los casos lo tendremos con los últimos ya que su masa está toda situada en el punto más alejado del eje imaginario de rotación (extremo de la biela). Circulando a 25 km/h con un pedal de 0.3 kg de masa su energía cinética de traslación vale:
 = 1/2*m*v^2 = 0.5*0.3*(6.94)^2 = 7.23 J
= 1/2*m*v^2 = 0.5*0.3*(6.94)^2 = 7.23 JPara calcular la energía cinética de rotación supondremos que se usan bielas de 175mm de largo y que pedaleamos con una cadencia de 80 pedaladas por minuto:
w=80 ppm –> 1.333rev/s —> 2*pi*1.333 rev/s = 8.37 rad/s
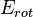 = 1/2*m*R^2*w^2 = 0.32 J
= 1/2*m*R^2*w^2 = 0.32 J0.32 J << 7.23 J
Es decir, el peso de unos pedales se puede considerar a efectos prácticos como el de cualquier otro componente que no gire y de misma masa. Esto se debe a un radio de giro y velocidad angular pequeños.
En el caso de unas bielas, por lógica, la energía rotacional es ínfima comparada a la de traslación ya que su masa se distribuye linealmente hasta el eje de giro. Se podía hacer una integral lineal y comprobar que es casi 2 órdenes de magnitud más pequeña que la de traslación.
Conclusión: que nadie vuelva a decir que reducir peso en bielas y pedales es más importante que en otra parte por el simple hecho que giran ¡Da igual de dónde lo restemos siempre que hablemos de la misma cantidad de peso!.
fuente: fernandoj

No hay comentarios:
Publicar un comentario